leetcode-144

144. 二叉树的前序遍历

给你二叉树的根节点 root ，返回它节点值的前序遍历。

示例 1：

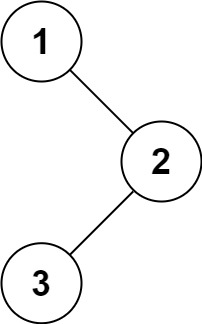
1 2	输入：root = [1,null,2,3] 输出：[1,2,3]

示例 2：

1 2	输入：root = [] 输出：[]

示例 3：

1 2	输入：root = [1] 输出：[1]

示例 4：

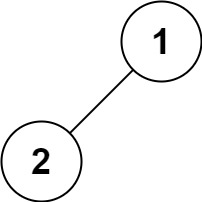
1 2	输入：root = [1,2] 输出：[1,2]

示例 5：

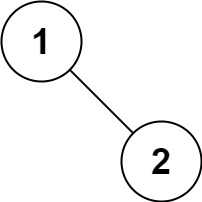
1 2	输入：root = [1,null,2] 输出：[1,2]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

方法一：递归

思路与算法

首先我们需要了解什么是二叉树的前序遍历：按照访问根节点——左子树——右子树的方式遍历这棵树，而在访问左子树或者右子树的时候，我们按照同样的方式遍历，直到遍历完整棵树。因此整个遍历过程天然具有递归的性质，我们可以直接用递归函数来模拟这一过程。

定义 preorder(root) 表示当前遍历到 root 节点的答案。按照定义，我们只要首先将 root 节点的值加入答案，然后递归调用 preorder(root.left) 来遍历 root 节点的左子树，最后递归调用 preorder(root.right) 来遍历 root 节点的右子树即可，递归终止的条件为碰到空节点。

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        dfs(root, ans);
        return ans;
    }

    private void dfs(TreeNode root, List<Integer> ans) {
        if (root == null) {return;}
        ans.add(root.val);
        dfs(root.left, ans);
        dfs(root.right, ans);
    }
}

复杂度分析

时间复杂度：O(n)，其中 nn 是二叉树的节点数。每一个节点恰好被遍历一次。

空间复杂度：O(n)，为递归过程中栈的开销，平均情况下为 O(logn)，最坏情况下树呈现链状，为 O(n)。

方法二：迭代

思路与算法

我们也可以用迭代的方式实现方法一的递归函数，两种方式是等价的，区别在于递归的时候隐式地维护了一个栈，而我们在迭代的时候需要显式地将这个栈模拟出来，其余的实现与细节都相同，具体可以参考下面的代码。

public class Solution2 {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        Deque<TreeNode> stack = new LinkedList<>();
        while (root != null || !stack.isEmpty()) {
            while (root != null) {
                ans.add(root.val);
                stack.offerLast(root);
                root = root.left;
            }
            root = stack.pollLast();
            assert root != null;
            root = root.right;
        }
        return ans;
    }
}

复杂度分析

时间复杂度：O(n)，其中 nn 是二叉树的节点数。每一个节点恰好被遍历一次。

空间复杂度：O(n)，为迭代过程中显式栈的开销，平均情况下为 O(logn)，最坏情况下树呈现链状，为 O(n)。

方法三：Morris 遍历

思路与算法

可以在线性时间内，只占用常数空间来实现前序遍历。这种方法由 J. H. Morris 在 1979 年的论文「Traversing Binary Trees Simply and Cheaply」中首次提出，因此被称为 Morris 遍历。

Morris 遍历的核心思想是利用树的大量空闲指针，实现空间开销的极限缩减。其前序遍历规则总结如下：

新建临时节点，令该节点为 root；
如果当前节点的左子节点为空，将当前节点加入答案，并遍历当前节点的右子节点；
如果当前节点的左子节点不为空，在当前节点的左子树中找到当前节点在中序遍历下的前驱节点：
- 如果前驱节点的右子节点为空，将前驱节点的右子节点设置为当前节点。然后将当前节点加入答案，并将前驱节点的右子节点更新为当前节点。当前节点更新为当前节点的左子节点。
- 如果前驱节点的右子节点为当前节点，将它的右子节点重新设为空。当前节点更新为当前节点的右子节点。
重复步骤 2 和步骤 3，直到遍历结束。

这样我们利用 Morris 遍历的方法，前序遍历该二叉树，即可实现线性时间与常数空间的遍历。

public class Solution3 {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        TreeNode cur = root, p;
        while (cur != null) {
            if (cur.left == null) {
                ans.add(cur.val);
                cur = cur.right;
            } else {
                p = cur.left;
                while (p.right != null && p.right != cur) {
                    p = p.right;
                }
                if (p.right == null) {
                    ans.add(cur.val);
                    p.right = cur;
                    cur = cur.left;
                } else {
                    p.right = null;
                    cur = cur.right;
                }
            }
        }
        return ans;
    }
}

复杂度分析

时间复杂度：O(n)，其中 n 是二叉树的节点数。没有左子树的节点只被访问一次，有左子树的节点被访问两次。

空间复杂度：O(1)。只操作已经存在的指针（树的空闲指针），因此只需要常数的额外空间。