给你一棵二叉搜索树,请你 按中序遍历 将其重新排列为一棵递增顺序搜索树,使树中最左边的节点成为树的根节点,并且每个节点没有左子节点,只有一个右子节点。
示例 1:
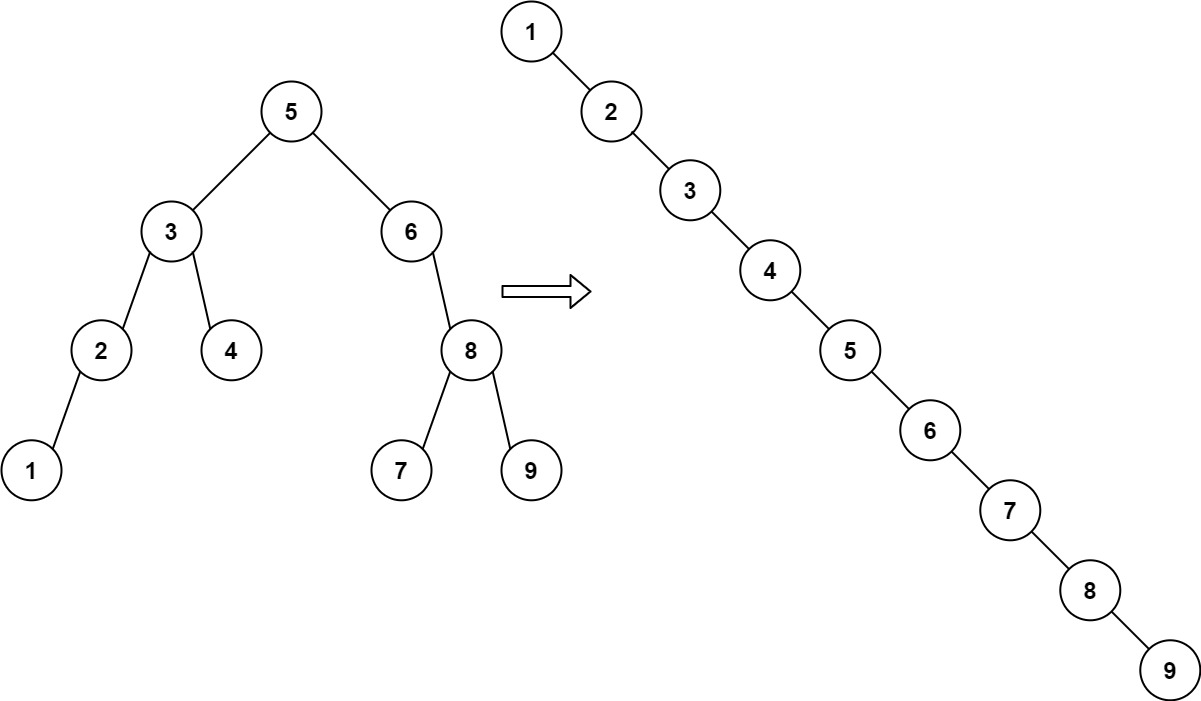
输入:root = [5,3,6,2,4,null,8,1,null,null,null,7,9]
输出:[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]
示例 2:
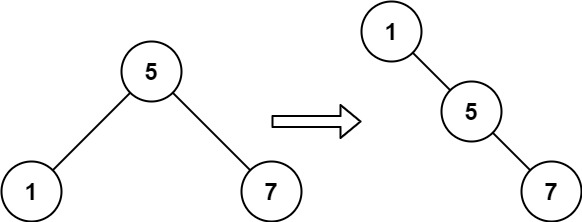
输入:root = [5,1,7]
输出:[1,null,5,null,7]
提示:
树中节点数的取值范围是 [1, 100]
0 <= Node.val <= 1000
方法一:中序遍历之后生成新的树
算法
题目要求我们返回按照中序遍历的结果改造而成的、只有右节点的等价二叉搜索树。我们可以进行如下操作:
先对输入的二叉搜索树执行中序遍历,将结果保存到一个列表中;
然后根据列表中的节点值,创建等价的只含有右节点的二叉搜索树,其过程等价于根据节点值创建一个链表。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| public class Solution {
public TreeNode increasingBST(TreeNode root) {
List<Integer> res = new ArrayList<>();
inorder(root, res);
TreeNode p = new TreeNode(-1);
TreeNode cur = p;
for (int val: res) {
cur.right = new TreeNode(val);
cur = cur.right;
}
return p.right;
}
public void inorder(TreeNode root, List<Integer> res) {
if (root == null) {
return;
}
inorder(root.left, res);
res.add(root.val);
inorder(root.right, res);
}
}
|
复杂度分析
时间复杂度:O(n),其中 n 是二叉搜索树的节点总数。
空间复杂度:O(n),其中 n 是二叉搜索树的节点总数。需要长度为 n 的列表保存二叉搜索树的所有节点的值。
方法二:在中序遍历的过程中改变节点指向
算法
方法一需要遍历一次二叉搜索树以后,然后再创建新的等价的二叉搜索树。事实上,还可以遍历一次输入二叉搜索树,在遍历的过程中改变节点指向以满足题目的要求。
在中序遍历的时候,修改节点指向就可以实现。具体地,当我们遍历到一个节点时,把它的左孩子设为空,并将其本身作为上一个遍历到的节点的右孩子。这里需要有一些想象能力。递归遍历的过程中,由于递归函数的调用栈保存了节点的引用,因此上述操作可以实现。下面的幻灯片展示了这样的过程。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| public class Solution2 {
private TreeNode res;
public TreeNode increasingBST(TreeNode root) {
TreeNode p = new TreeNode(-1);
res = p;
inorder(root);
return p.right;
}
private void inorder(TreeNode root) {
if (root == null) {
return;
}
inorder(root.left);
res.right = root;
root.left = null;
res = root;
inorder(root.right);
}
}
|
复杂度分析
- 时间复杂度:O(n),其中 n是二叉搜索树的节点总数。
- 空间复杂度:O(n)。递归过程中的栈空间开销为 O(n)。
递归的迭代写法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public class Solution3 {
public TreeNode increasingBST(TreeNode root) {
TreeNode node = new TreeNode();
TreeNode cur = node;
Deque<TreeNode> stack = new LinkedList<>();
while (root != null || !stack.isEmpty()) {
while (root != null) {
stack.addLast(root);
root = root.left;
}
root = stack.pollLast();
cur.right = root;
cur = root;
root.left = null;
root = root.right;
}
return node.right;
}
}
|

